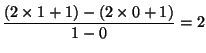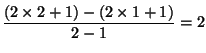2つの変数x, y の間に,y = ax +b (ただし,a, b は定数)で表される関係があるとき,y はx の1次関数という。1次関数y = ax +b のグラフは,傾きa, 切片b の直線である。
y = 2x +1のグラフ
このグラフは,x の値に対応するy の値をもとめて,座標平面上に点をとり,それらの点をむすんでいくと,y 軸と(0,1)で交わり,傾きが2である直線になる。
y = ax (a ≠0)のグラフ
このグラフは,原点Oを通り,傾きがa の直線である。ここで,a >0のとき,右上がりの直線,a <0のとき,右下がりの直線である。また,a の絶対値が大きくなるにつれて,x 軸とのなす角が大きくなる。
y = ax +b (a, b は定数,a ≠0)のグラフ
このグラフは,傾きがa で,y 軸上の切片がb である直線である。また,このグラフは,y = ax のグラフをy 軸方向に,b だけ平行移動したものである。
1次関数y = ax +b の値の変化の割合
一般に,x の関数y について,x がある値からある値に増加するときの変化の割合は, である。
である。
たとえば,y = 2x +1で,x = 0からx = 1までの変化の割合は,

x = 1からx = 2までの変化の割合は,

で,変化の割合は2で等しい。一般に,1次関数y = ax +b の変化の割合は一定で,x の係数a に等しい。
1次関数の式のもとめ方
(1)1点と傾きがあたえられているとき。
1点(3,2)を通り,傾きが1である直線の式は,y = ax +b とおいて,a, b を決めればよい。
点(3,2)を通るから 2 = 3a +b …(ア)
また直線の傾きが1だから a = 1…(イ)
(ア)と(イ)より,a = 1, b = -1
よって,もとめる式は,y = x -1
(2)2点があたえられているとき。
2点(2,-3),(-2,5)を通る直線の式は,
y = ax +b とおくと,-3 = 2a +b …(ア)
5 = -2a +b …(イ)
(ア)と(イ)より,a = -2, b = 1
よって,もとめる式は,y = -2x +1
 である。
である。