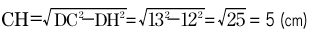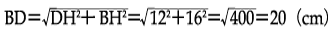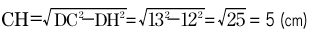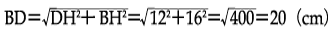＊＊さんへいほうのていり【三平方の定理】

直角三角形の直角をはさむ2辺(へん）の長さをa， b，斜辺(しゃへん）の長さをc とすれば，a² + b² ＝ c² となる。これを三平方の定理，またはピタゴラスの定理という。

3辺(ぺん）の比(ひ）が，3：4：5， 5：12：13などになる三角形は，直角三角形である。

平行四辺形(へいこうしへんけい）ABCDにおいて，AB ＝ 13cm，BC ＝ 11cm，∠ABCが鋭角(えいかく）であるとき，対角線BDの長さをもとめよ。ただし，この平行四辺形の面積を132cm²とする。

点DからBCに垂線(すいせん）をおろし，BCの延長上と交わる点をHとする。平行四辺形ABCDの面積が132cm²で，辺BCの長さが11cmであるから，DHの長さは，

132÷11で12cm。

直角三角形DCHで，三平方の定理を用いてCHの長さを求めると，

直角三角形DBHでDH ＝ 12（cm），BH ＝ BC+CH ＝ 11+5 ＝ 16（cm）であるから，

20cm