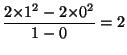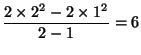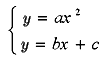2つの変数x, y の間に,y はx の2次式で表されるという関係があるとき,y はx の2次関数という。2次関数の最も一般な形は,y = ax 2 + bx + c (ただし,a, b, c は定数,a ≠0)である。
y = ax 2 (a ≠0)のグラフ
このグラフは,原点Oを通り,y 軸について対称な曲線である。この曲線を放物線といい,対称軸を放物線の軸,軸と放物線の交点を放物線の頂点という。ここでは,原点Oが放物線の頂点である。またa については,a >0のとき,上に開いた放物線で,グラフはx 軸より下にはあらわれない。a <0のとき,下に開いた放物線で,グラフはx 軸より上にはあらわれない。さらに,a の絶対値が大きいほど,グラフはy 軸に近づく。
2次関数 y = ax 2 の変化の割合
一般に,x の関数y について,変化の割合は, である。
である。
たとえば,y = 2x 2で,
x = 0から1までの変化の割合は,

x = 1から2までの変化の割合は,

で,変化の割合は異なる。変化の割合は,1次関数ではつねに一定であるが,2次関数では一定でない。
2次関数と1次関数の交点
y = ax 2 とy = bx +c のグラフの交点の座標は,連立方程式

の解である。
ここで,y を消去すると,ax 2 = bx +c となるが,この解は両式のグラフの交点のx 座標である。このようにして,2つのグラフの交点をもとめることができる。
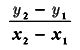 である。
である。