＊＊れんりつほうていしき【連立方程式】

同時になりたつことを条件(じょうけん）として，2つ以上(いじょう）の方程式(ほうていしき）を組み合わせたもの。連立方程式(れんりつほうていしき）は｛を用いてその組み合わせを表す。連立方程式(れんりつほうていしき）の各方程式(かくほうていしき）を同時になりたたせる文字の値(あたい）の組を連立方程式(れんりつほうていしき）の解(かい），解(かい）をもとめることを「連立方程式(れんりつほうていしき）を解(と）く」という。◇連立方程式(れんりつほうていしき）の各項(かくこう）のうち，最(もっと）も高い次数をその連立方程式(れんりつほうていしき）の次数といい，連立方程式(れんりつほうていしき）の中にふくまれている文字の数を元(げん）という。

例題

次の連立方程式(れんりつほうていしき）を解(と）きなさい。

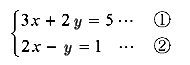
上の連立(れんりつ）（2元1次）方程式(ほうていしき）を解(と）くには，2つの文字のうちいずれか一方，たとえば，y をふくまない方程式(ほうていしき）をつくり，x について解(と）く。そのあと，y をもとめる方法(ほうほう）で解(と）けばよい。1つの文字をふくまない方程式(ほうていしき）をつくることは消去するという。文字を消去するには，加減法(かげんほう）と代入法(だいにゅうほう）がある。

解き方〔加減法(かげんほう）による〕

(1)+(2)×2をつくれば，y が消去され，

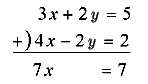
x ＝ 1………(3)

この(3)を(2)に代入して，y ＝ 1がもとめられる。

解き方〔代入法(だいにゅうほう）による〕

(2)から，

y ＝ 2x -1………(4)

(4)を(1)のy に代入すると，

3x +2（2x -1）＝ 5

7x -2 ＝ 5

x ＝ 1………(5)

(5)を(4)に代入すれば，y がもとめられる。

y ＝ 1

解き方〔グラフによる〕

2つの方程式(ほうていしき）のグラフから，交点をもとめる。

答

x ＝ 1，y ＝ 1